Optimal Rocket Launch
Course: MAE 270C Optimal Control
The purpose of the class project was to derive an optimal controller for a rocket launch with both constrained and non-constrained terminal states.
About the course:
MAE 270C covers both linear and nonlinear optimal control. Specifically covered are applications of variational methods, Pontryagin’s maximum principle, Hamilton/Jacobi/Bellman equation (dynamic programming) to optimal control of dynamic systems modeled by nonlinear ordinary differential equations.
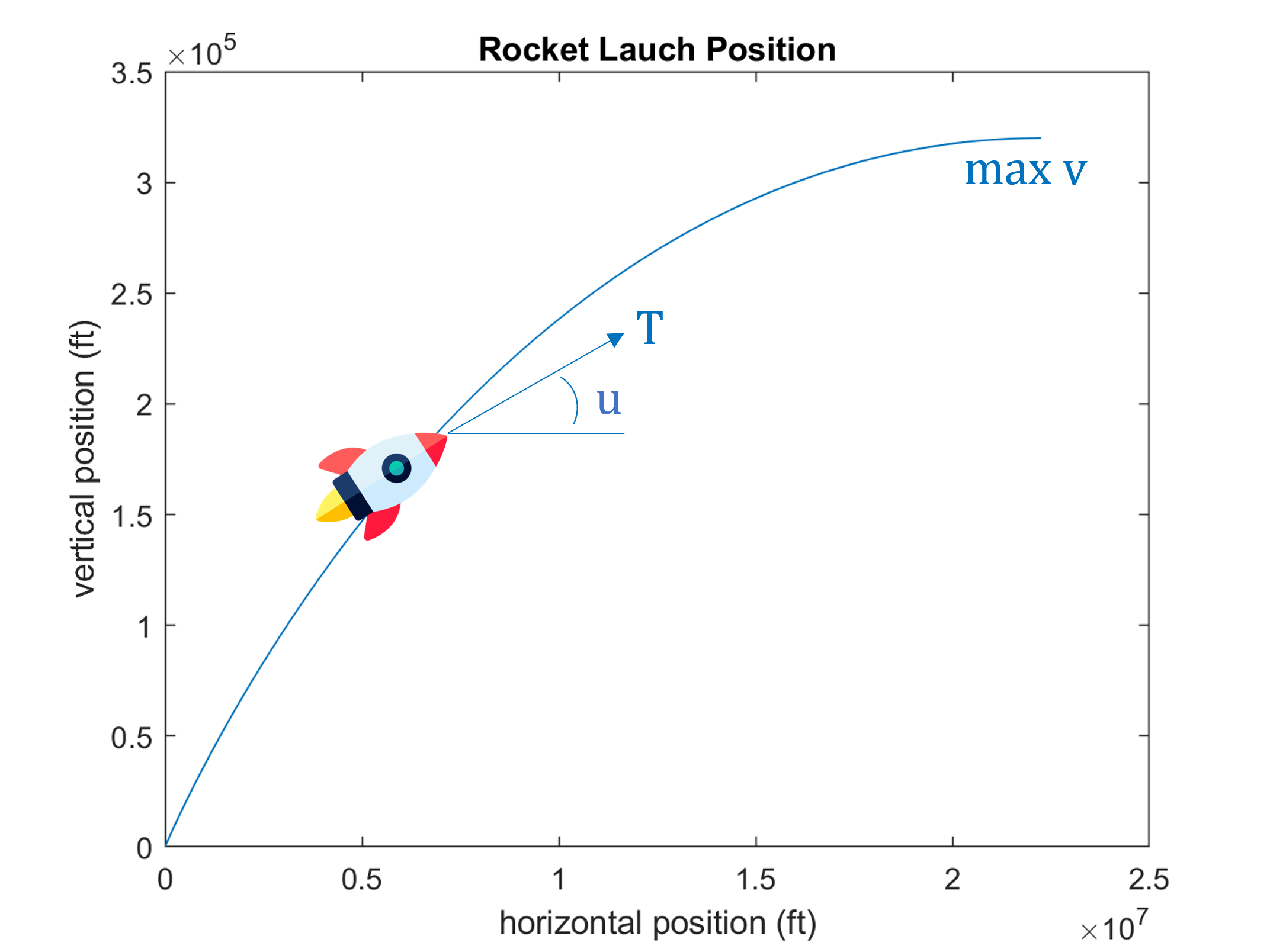
Abstract:
This work formulates a rocket launch as a two dimensional optimal control problem. The object is to maximize the final horizontal velocity subject to terminal state constraints. The steepest ascent approach is used for numerically solving this optimization. Through simulation in MATLAB, the optimal horizontal velocity was found to be 49863 ft/s and the optimal control input was observed to have near-linear behavior through time.