Batch Normalization on the Hessian of a Shallow Network
Course: MATH 273A - Optimization and Calculus of Variations - Basic Optimization Theory
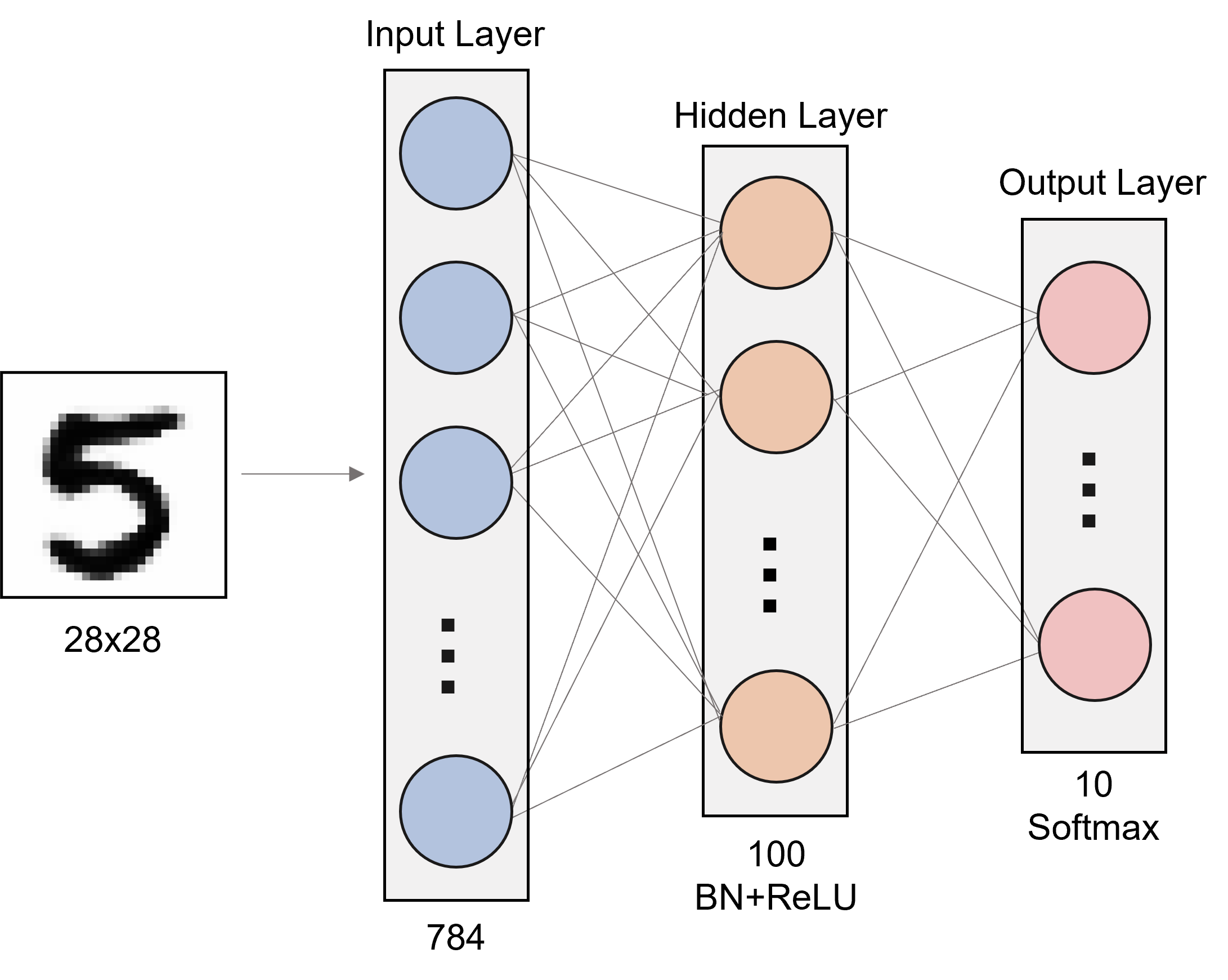
The purpose of this project was to investigate why batch normalization leads to faster convergence through experimental results on a two layer neural network and analyses on the loss function's Hessian.
About the course:
MATH 273A is an introduction to optimization and various numerical optimization methods. Specific topics included basic optimization theory, recognition of solutions, and geometry of optimization. Some convex analysis, separation hyperplane, and duality theory. Basic optimization algorithms and their rates of convergence.
Abstract:
The difficulty of training deep neural networks has led to a proliferation of optimization algorithms which seek to simplify learning and improve convergence. Batch normalization is one of the most well known, and implemented methods to optimize deep neural networks. This study seeks to understand why batch normalization leads to faster convergence through experimental results and analyses on the loss function’s Hessian. Two shallow networks with and without batch normalization were trained on the MNIST Dataset and evaluated. We hypothesize that batch normalization leads to faster convergence due to the improvement of the Hessian’s condition number, and we support this hypothesis with the demonstration of a reduced pseudocondition number and improved convergence when batch normalization is introduced.